Introducing the Binomial Heap data structure 3 – Arrays, collections and data structures

Implementing unionHeap(BinomialHeap heap)

Consider two Binomial Heaps (H1 and H2). The goal of the union operation is to create H3 by unifying H1 with H2. Let’s assume that H1 (having a conventional string representation used by our application as 31 22 [ 40 ] 8 [ 13 [ 24 ] 11 ]) and H2 (55 24 [ 45 ] 3 [ 7 [ 29 [ 40 ] 9 ] 5 [ 37 ] 18 ]) are those from the following figure:

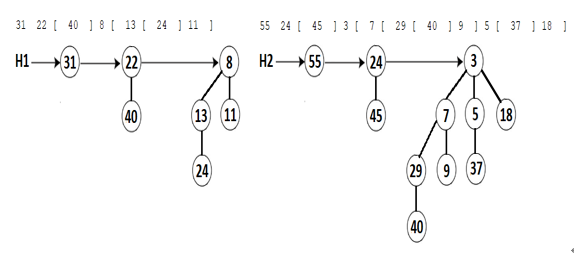
Figure 5.31 – Two Binomial Heaps, H1 and H2

The contract of unification starts with an initial merging of H1 and H2 in the order of their degrees. In our case the merge operation produces the following output:

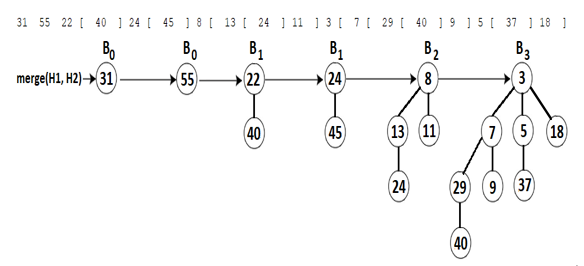
Figure 5.31 – Merging H1 and H2

This operation is performed by the following helper method:

private Node merge(BinomialHeap h1, BinomialHeap h2) {
  if (h1.head == null) {
    return h2.head;
  } else if (h2.head == null) {
    return h1.head;
  } else {
    Node headIt;
    Node h1Next = h1.head;
    Node h2Next = h2.head;
    if (h1.head.degree <= h2.head.degree) {
      headIt = h1.head;
      h1Next = h1Next.sibling;
    } else {
      headIt = h2.head;
      h2Next = h2Next.sibling;
    }
    Node tail = headIt;
    while (h1Next != null && h2Next != null) {
      if (h1Next.degree <= h2Next.degree) {
        tail.sibling = h1Next;
        h1Next = h1Next.sibling;
      } else {
        tail.sibling = h2Next;
        h2Next = h2Next.sibling;
      }
      tail = tail.sibling;
    }
    if (h1Next != null) {
      tail.sibling = h1Next;
    } else {
      tail.sibling = h2Next;
    }
    return headIt;
  }
}

Next, we need to combine the Binomial Trees of the same order. While we traverse the roots of the merged heaps (here, 31, 55, 22, 24, 8, and 3) we use three pointers denoted as PREV-X  (the previous node of the current node), X  (the current node), and NEXT-X (the next node of the current node). These pointers help us to solve the following four cases:

Case 1: The X and NEXT-X have different orders. In this case, we just move the X pointer ahead.

Case 2: The X, NEXT-X, and NEXT-NEXT-X have the same order. In this case, we just move the X pointer ahead.

Case 3: The X and NEXT-X have the same order different from NEXT-NEXT-X. And, if X.KEY <= NEXT-X.KEY then NEXT-X becomes the child of X.

Case 4: The X and NEXT-X have the same order different from NEXT-NEXT-X. And, if X.KEY > NEXT-X.KEY then X becomes the child of NEXT-X.

If we apply these four cases to our example that we notice that after merging H1 and H2, we are in Case 3 since X and NEXT-X have the same order (B0) which is different from the order of NEXT-NEXT-X (which is B1) and X.KEY = 31 < 55 = NEXT-X.KEY. So, NEXT-X becomes the child of X as in the following figure:

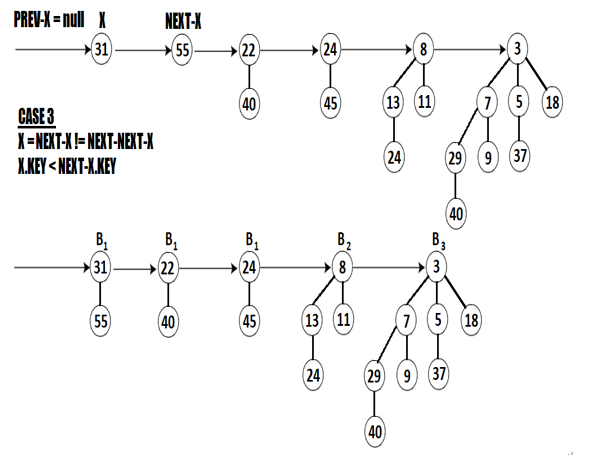
Figure 5.32 – Applying Case 3

Going further, we notice that X, NEXT-X, and NEXT-NEXT-X have the same order B1. This means that we are in Case 2, so we have to move the X pointer forward as in the following figure:

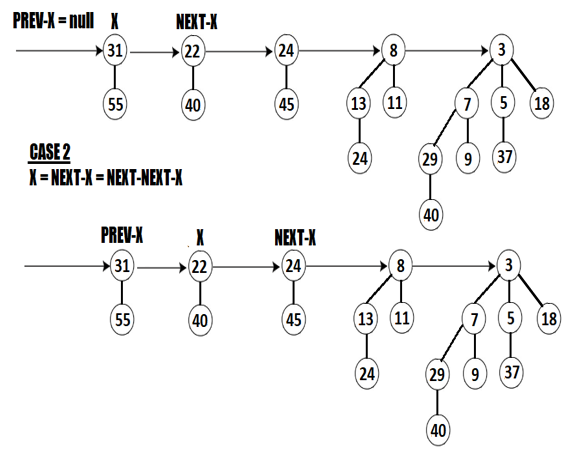
Figure 5.33 – Applying Case 2

Next, we are in Case 3 again. We have that X and NEXT-X have the same order (B1) which is different from the order of NEXT-NEXT-X (B2). And, we also have that X.KEY = 22 < 24 = NEXT-X.KEY, so X-NEXT becomes the child of X as in the following figure:

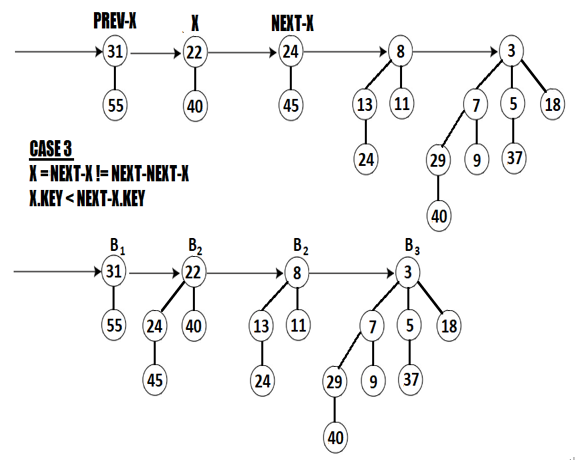
Figure 5.34 – Applying Case 3 again

Next, we are in Case 4. We have that X and NEXT-X have the same order (B2) which is different from the order of NEXT-NEXT-X (B3). And, we also have that X.KEY = 22 > 8 = NEXT-X.KEY, so X becomes the child of X-NEXT as in the following figure:

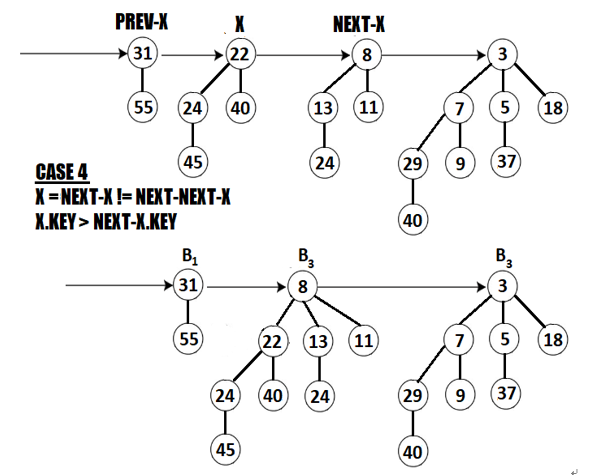
Figure 5.36 – Applying Case 4

Next, we are in Case 4 again. We have that X and NEXT-X have the same order (B3) which is different from the order of NEXT-NEXT-X (null). And, we also have that X.KEY = 8 > 3 = NEXT-X.KEY, so X becomes the child of X-NEXT as in the following figure:

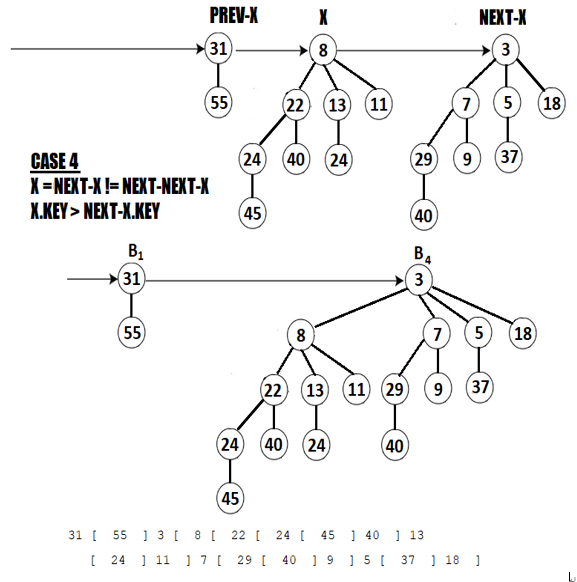
Figure 5.37 – Applying Case 4 again

At this point, none of the four cases is valid so this is the final form of the Binomial Heap.Based on this example, we can implement the union operation as follows (notice the highlighted cases directly on the code):

private Node unionHeap(BinomialHeap heap) {
  Node mergeHeap = merge(this, heap);     
  head = null;
  heap.head = null;
  if (mergeHeap == null) {
    return null;
  }
  Node previousNode = null;
  Node currentNode = mergeHeap;
  Node nextNode = mergeHeap.sibling;
  while (nextNode != null) {
    if (currentNode.degree != nextNode.degree
        || (nextNode.sibling != null
        && nextNode.sibling.degree == currentNode.degree)) {
[C:1,2] previousNode = currentNode;
[C:1,2] currentNode = nextNode;
    } else {
      if (currentNode.key < nextNode.key) {
[C:3]   currentNode.sibling = nextNode.sibling;
[C:3]   linkNodes(currentNode, nextNode);
[C:4] } else {
[C:4]   if (previousNode == null) {
[C:4]     mergeHeap = nextNode;
[C:4]   } else {
[C:4]     previousNode.sibling = nextNode;
[C:4]   }
[C:4]
[C:4]   linkNodes(nextNode, currentNode);
[C:4]   currentNode = nextNode;
      }
    }
    nextNode = currentNode.sibling;
  }
  return mergeHeap;
}

The linkNodes() method is a helper method that links the current node with the next node:

private void linkNodes(Node minNodeTree, Node other) {
  other.parent = minNodeTree;
  other.sibling = minNodeTree.child;
  minNodeTree.child = other;
  minNodeTree.degree++;
}

Done! You can find the complete application in the bundled code.