Introducing the Binomial Heap data structure – Arrays, collections and data structures

116. Introducing the Binomial Heap data structure

A Binomial Heap data structure is a set composed of Binomial Trees. Each Binomial Tree is a Min Heap which means that it follows the min-heap property. In a nutshell, a heap is a Min Heap if its items are in descending order which means that the minimum item is the root (more details are available in The Complete Coding Interview Guide in Java book).In a nutshell, a Binomial Tree is ordered and typically is defined in a recursive fashion. It is denoted as Bk, where k implies the following properties:

A Binomial Tree has 2k nodes The height of a Binomial Tree is equal to k The root of a Binomial Tree has the degree k which is the greatest degree A B0 Binomial Tree has a single node. A B1 Binomial Tree has two B0 trees, and one of them is a left subtree of the other one. A B2 has two B1, and one B1 is the left subtree of the other one. In general, a Bk Binomial Tree contains two Binomial Trees Bk-1, and one of the Bk-1 is the left subtree of the other one (two Bk-1 are linked to composed Bk). In the following figure, you can see B0, B1, B2, B3, and B4.

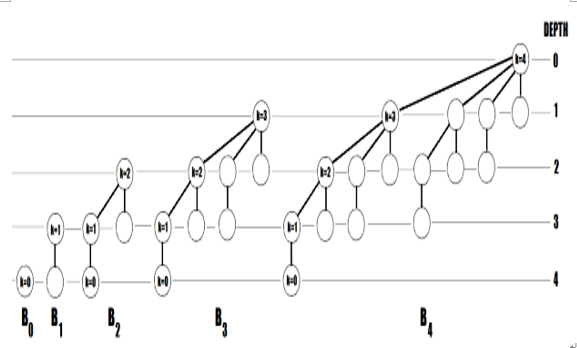
Figure 5.27 – Binomial Trees B 0 -B 4

The goals of a Binomial Heap from Big O perspective are listed in the following figure:

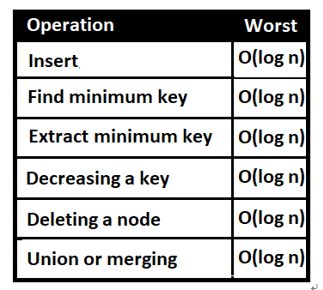
Figure 5.28 – Big O for Binomial Heap

In the following figure, you can see a sample of a Binomial Heap. The roots of the Binomial Trees (here, 9, 1, and 7) within a Binomial Heap are represented via a linked list referred to as the root list.

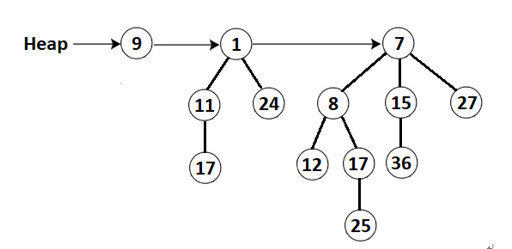
Figure 5.29 – Binomial Heap sample

In other words, as you can easily intuit from this figure, a Binomial Heap is an extension (or a flavor) of a Binary Heap with provide high performance for merging or union two heaps and fits perfectly for implementing priority queues.Based on this figure, we can define the skeleton of a Binomial Heap as follows:

public class BinomialHeap {
  private Node head;
  private final class Node {
    private int key;
    private int degree;
    private Node parent;
    private Node child;
    private Node sibling;
    public Node() {
      key = Integer.MIN_VALUE;
    }
    public Node(int key) {
      this.key = key;
    }
    …
  }
  …
}

If we represent the relevant part of a Node as a diagram we obtain the following figure (here, you can see the internal structure of a Node for items 11 and 25):

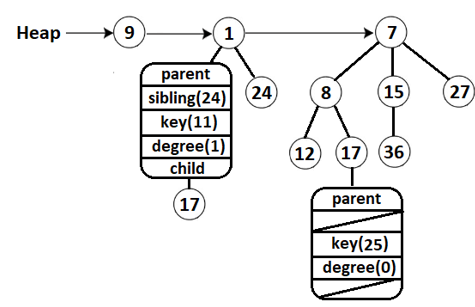
Figure 5.30 – Expanding a Node

Now that we have the main structure of a Binomial Heap, let’s cover several operations.

Implementing insert(int key)

Inserting a new key in a Binomial Heap is a two-step operation. In the first step, we create a new heap containing only the given key (a Node wrapping the given key). Second we union the current heap with this newly created heap as follows:

public void insert(int key) {
  Node node = new Node(key);
  BinomialHeap newHeap = new BinomialHeap(node);
  head = unionHeap(newHeap);
}

The union operation is depicted as the last operation of this section.