Introducing the K-D-trees data structure 2 – Arrays, collections and data structures

Done! So inserting has two simple rules:We compare components alternatively starting with x. At level one, we compare x, at level two, we compare y, at level three we compare x, at level four we compare y, and so on.When comparing (x1, y1) with (x2, y2), if x2 >= x1 or y2 >= y1 (depending on which component is compared) then the (x2,y2) node goes to the right (x1,y1), otherwise to the left.Based on these statements the implementation of a 2-D model is straightforward:

public void insert(double[] coords) {
  root = insert(root, coords, 0);
}
private Node insert(Node root, double[] coords, int depth) {
  if (root == null) {
    return newNode(coords);
  }
  int cd = depth % 2;
  if (coords[cd] < root.coords[cd]) {
    root.left = insert(root.left, coords, depth + 1);
  } else {
    root.right = insert(root.right, coords, depth + 1);
  }
  return root;
}

Another approach for inserting in a K-D Tree relies on a sorting algorithm for sorting the coordinates. This implementation is not available here.

Find the nearest neighbor

Finding the nearest neighbor is the classical operation performed on a K-D Tree. We have a given point (x, y), and we want to know what is the nearest point from the K-D Tree. For instance, we may want to find the nearest neighbor of (4, 4) – check the following figure.

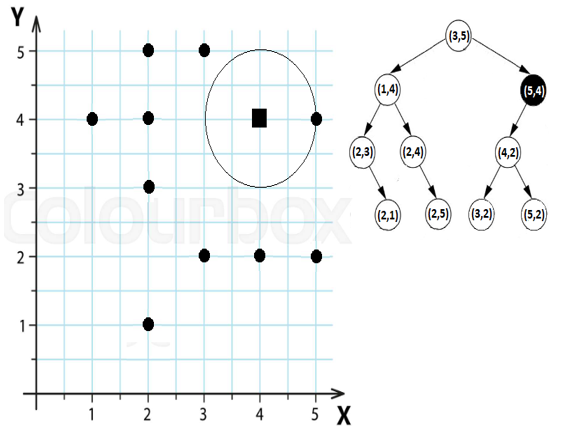
Figure 2.25 – Find the nearest neighbor of (4, 4)

The nearest neighbor of (4, 4) is (5, 4). In a nutshell, finding the nearest neighbor is about finding the shortest distance from the given point to any other point present in the K-D Tree. We start from the root and compute the distance between the given point (or target node) and the current node. The shortest distance wins. The implementation starts like this:

public double[] findNearest(double[] coords) {
  Node targetNode = newNode(coords);
  visited = 0;
  foundDistance = 0;
  found = null;
  nearest(root, targetNode, 0);
  return found.coords.clone();
}

And, the nearest() method is a recursive solution for finding the minimum distance:

private void nearest(Node root, Node targetNode, int index) {
  if (root == null) {
    return;
  }
  visited++;
  double theDistance = root.theDistance(targetNode);
  if (found == null || theDistance < foundDistance) {
    foundDistance = theDistance;
    found = root;
  }
  if (foundDistance == 0) {
    return;
  }
  double rootTargetDistance = root.get(index) –
      targetNode.get(index);
  index = (index + 1) % 2;
  nearest(rootTargetDistance > 0 ?
    root.left : root.right, targetNode, index);
  if (rootTargetDistance *
          rootTargetDistance >= foundDistance) {
    return;
  }
  nearest(rootTargetDistance > 0 ?
    root.right : root.left, targetNode, index);
}

In the bundled code, you can find the missing parts such as the method for computing the distance between two points.Searching and deleting from a K-D Tree is similar to performing these operations on a BST, so nothing new.Challenge yourself to implement a 3-D Tree, so for point of type (x, y, z).