Introducing the Splay Tree data structure – Arrays, collections and data structures

120. Introducing the Splay Tree data structure

A Splay Tree is a flavor of Binary Search Tree (BST). Its particularity consists of the fact that it is a self-balancing tree that places the recently accessed items at the root level.The splaying operation or splaying an item is a process that relies on tree rotations meant to bring the item to the root position. Every operation on the tree is followed by splaying.So, the goal of splaying is to bring the most recently used item closer to the root. This means that subsequent operations on these items will perform faster.The splaying operation relies on six rotations:

Zig Rotation – the tree rotates to the right (every node rotates to the right)

Zag Rotation – the tree rotates to the left (every node rotates to the left)

Zig – Zig Rotation – double Zig rotation (every node moves twice to the right)

Zag – Zag Rotation – double Zag rotation (every node moves twice to the left)

Zig – Zag Rotation – a Zig rotation followed by a Zag

Zag – Zig Rotation – a Zag rotation followed by a Zig

In the bundled code, you can find an implementation of a Splay Tree. Moreover, you can use this visualizer: https://www.cs.usfca.edu/~galles/visualization/SplayTree.html.

121. Introducing the Interval Tree data structure

An Interval Tree is a flavor of Binary Search Tree (BST). Its particularity consists of the fact that it holds intervals of values. Beside the interval itself, a Node of an Interval Tree holds the maximum value of the current interval and the maximum value of the subtree rooted with this Node.In code lines, an Interval Tree is shaped as follows:

public class IntervalTree {
  private Node root;
  public static final class Interval {
    private final int min, max;
    public Interval(int min, int max) {
      this.min = min;
      this.max = max;
    }
    …
  }
  private final class Node {
    private final Interval interval;
    private final Integer maxInterval;
    private Node left;
    private Node right;
    private int size;
    private int maxSubstree;
    Node(Interval interval, Integer maxInterval) {
      this.interval = interval;
      this.maxInterval = maxInterval;
      this.size = 1;
      this.maxSubstree = interval.max;
    }
  }
…
}

Let’s consider that we have the following intervals of integers: [4, 7], [1, 10], [7, 23], [6, 8], [9, 13], [2, 24].

Implementing insert(Interval interval)

The first interval ([4, 7]) becomes the root of the tree. Next, we compare the interval [1, 10] with [4, 7] by comparing the left side of the interval. Since 1 < 4, the interval [1, 10] goes to the left of the root.Next, we compare the interval [7, 23] with [4, 7]. Since 7 > 4, the interval [7, 23] goes to the right of [4, 7]. Applying the same logic for the rest of the interval will result in the following tree:

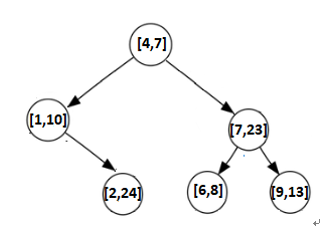
Figure 5.45 – The interval tree

The previous logic (insert operation O(log n)) is materialized in code lines as follows:

public void insert(Interval interval) {
  root = insert(root, interval);
}
private Node insert(Node root, Interval interval) {
  if (root == null) {
    return new Node(interval, interval.max);
  }
  if (interval.min < root.interval.min) {
    root.left = insert(root.left, interval);
  } else {
    root.right = insert(root.right, interval);
  }
  if (root.maxSubstree < interval.max) {
    root.maxSubstree = interval.max;
  }
  return root;
}

Other operations specific to an interval tree are: searching the intervals that overlap the given interval (O(log n)) and deleting (O (log n)). You can find the implementations in the bundled code.